Univariate Bijections
Background
Normalizing Flows are a family of methods for constructing flexible distributions. As mentioned in the introduction, Normalizing Flows can be seen as a modern take on the change of variables method for random distributions, and this is most apparent for univariate bijections. Thus, in this first section we restrict our attention to representing univariate distributions with bijections.
The basic idea is that a simple source of noise, for example a variable with a standard normal distribution, , is passed through a bijective (i.e. invertible) function, to produce a more complex transformed variable . For such a random variable, we typically want to perform two operations: sampling and scoring. Sampling is trivial. First, we sample , then calculate . Scoring , or rather, evaluating the log-density , is more involved. How does the density of relate to the density of ? We can use the substitution rule of integral calculus to answer this. Suppose we want to evaluate the expectation of some function of . Then,
where denotes the support of , which in this case is . Crucially, we used the fact that is bijective to apply the substitution rule in going from the first to the second line. Equating the last two lines we get,
Inituitively, this equation says that the density of is equal to the density at the corresponding point in plus a term that corrects for the warp in volume around an infinitesimally small length around caused by the transformation.
If is cleverly constructed (and we will see several examples shortly), we can produce distributions that are more complex than standard normal noise and yet have easy sampling and computationally tractable scoring. Moreover, we can compose such bijective transformations to produce even more complex distributions. By an inductive argument, if we have transforms , then the log-density of the transformed variable is
where we've defined , for convenience of notation. In the following section, we will see how to generalize this method to multivariate .
Fixed Univariate Bijectors
FlowTorch contains classes for representing fixed univariate bijective transformations. These are particularly useful for restricting the range of transformed distributions, for example to lie on the unit hypercube. (In the following sections, we will explore how to represent learnable bijectors.)
Let us begin by showing how to represent and manipulate a simple transformed distribution,
You may have recognized that this is by definition, .
We begin by importing the relevant libraries:
import torch
import flowtorch.bijectors as bij
import flowtorch.distributions as dist
import matplotlib.pyplot as plt
import seaborn as sns
A variety of bijective transformations live in the flowtorch.bijectors module, and the classes to define transformed distributions live in flowtorch.distributions. We first create the base distribution of and the class encapsulating the transform :
dist_x = torch.distributions.Independent(
torch.distributions.Normal(torch.zeros(1), torch.ones(1)),
1
)
bijector = bij.Exp()
The class bij.Exp derives from bij.Fixed and defines the forward, inverse, and log-absolute-derivative operations for this transform,
In general, a bijector class defines these three operations, from which it is sufficient to perform sampling and scoring. We should think of a bijector as a plan to construct a normalizing flow rather than the normalizing flow itself - it requires being instantiated with a concrete base distribution supplying the relevant shape information,
dist_y = dist.Flow(dist_x, bijector)
This statement returns the object dist_y of type flowtorch.distributions.Flow representing an object that has an interface compatible with torch.distributions.Distribution. We are able to sample and score from dist_y object using its methods .sample, .rsample, and .log_prob.
Now, plotting samples from both the base and transformed distributions to verify that we that have produced the log-normal distribution:
plt.subplot(1, 2, 1)
plt.hist(dist_x.sample([1000]).numpy(), bins=50)
plt.title('Standard Normal')
plt.subplot(1, 2, 2)
plt.hist(dist_y.sample([1000]).numpy(), bins=50)
plt.title('Standard Log-Normal')
plt.show()
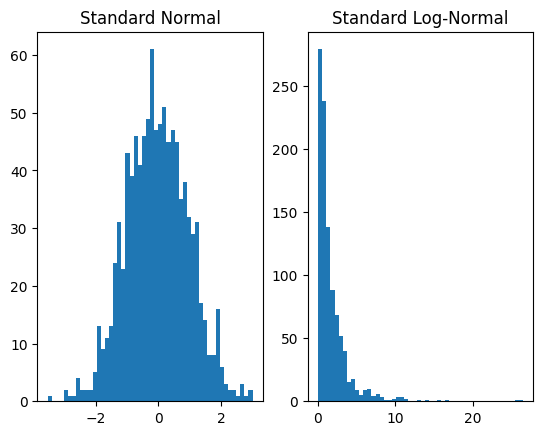
or rather, . In FlowTorch this is accomplished, e.g. for , as follows:
bijectors = bij.Compose([
bij.AffineFixed(loc=3, scale=0.5),
bij.Exp()])
dist_y = dist.Flow(dist_x, bijector)
plt.subplot(1, 2, 1)
plt.hist(dist_x.sample([1000]).numpy(), bins=50)
plt.title('Standard Normal')
plt.subplot(1, 2, 2)
plt.hist(dist_y.sample([1000]).numpy(), bins=50)
plt.title('Log-Normal')
plt.show()
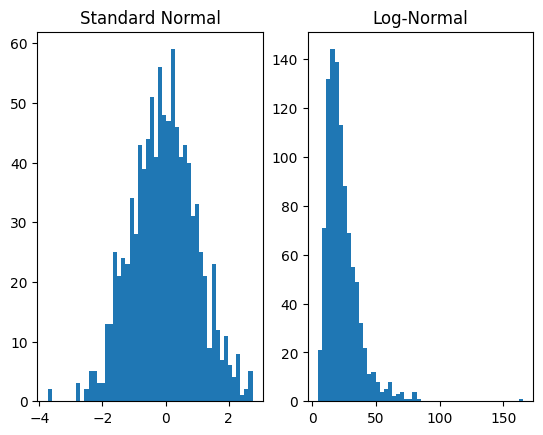
The class bij.Compose combines multiple Bijectors with function composition to produce a single plan for a Normalizing Flow, which is then intiated in the regular way. For the forward operation, transformations are applied in the order of the list. In this case, first AffineFixed is applied to the base distribution and then Exp.
Learnable Univariate Bijectors
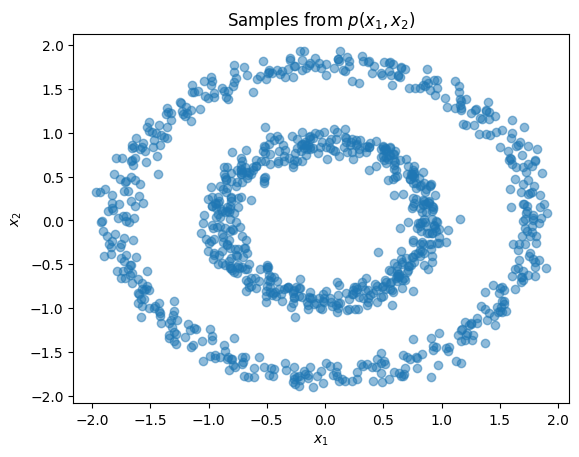
Having introduced the interface for bijections and transformed distributions, we now show how to represent learnable transforms and use them for density estimation. Our dataset in this section and the next will comprise samples along two concentric circles. Examining the joint and marginal distributions:
import numpy as np
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
n_samples = 1000
X, y = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
X = StandardScaler().fit_transform(X)
plt.title(r'Samples from $p(x_1,x_2)$')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.scatter(X[:,0], X[:,1], alpha=0.5)
plt.show()
plt.subplot(1, 2, 1)
sns.distplot(X[:,0], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2})
plt.title(r'$p(x_1)$')
plt.subplot(1, 2, 2)
sns.distplot(X[:,1], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2})
plt.title(r'$p(x_2)$')
plt.show()

We will learn the marginals of the above distribution using a learnable transform, bij.Spline, defined on a two-dimensional input:
dist_x = torch.distributions.Independent(
torch.distributions.Normal(torch.zeros(2), torch.ones(2)),
1
)
bijector = bij.Spline()
dist_y = dist.Flow(dist_x, bijector)
bij.Spline passes each dimension of its input through a separate monotonically increasing function known as a spline. From a high-level, a spline is a complex parametrizable curve for which we can define specific points known as knots that it passes through and the derivatives at the knots. The knots and their derivatives are parameters that can be learnt, e.g., through stochastic gradient descent on a maximum likelihood objective, as we now demonstrate:
optimizer = torch.optim.Adam(dist_y.parameters(), lr=1e-2)
for step in range(steps):
optimizer.zero_grad()
loss = -dist_y.log_prob(X).mean()
loss.backward()
optimizer.step()
if step % 200 == 0:
print('step: {}, loss: {}'.format(step, loss.item()))
step: 0, loss: 2.682476758956909
step: 200, loss: 1.278384804725647
step: 400, loss: 1.2647961378097534
step: 600, loss: 1.2601449489593506
step: 800, loss: 1.2561875581741333
step: 1000, loss: 1.2545257806777954
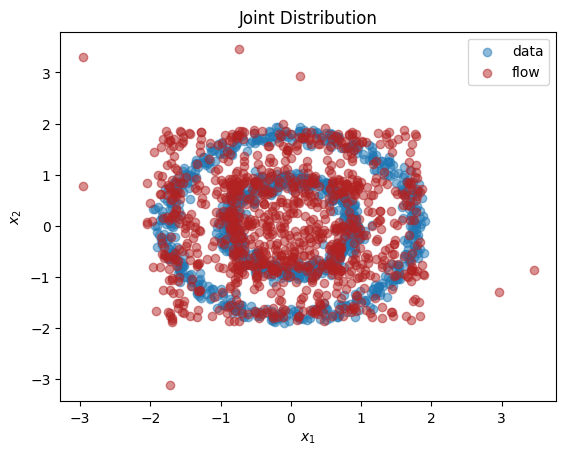
Plotting samples drawn from the transformed distribution after learning:
X_flow = dist_y.sample(torch.Size([1000,])).detach().numpy()
plt.title(r'Joint Distribution')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.scatter(X[:,0], X[:,1], label='data', alpha=0.5)
plt.scatter(X_flow[:,0], X_flow[:,1], color='firebrick', label='flow', alpha=0.5)
plt.legend()
plt.show()
plt.subplot(1, 2, 1)
sns.distplot(X[:,0], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,0], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_1)$')
plt.subplot(1, 2, 2)
sns.distplot(X[:,1], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,1], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_2)$')
plt.show()
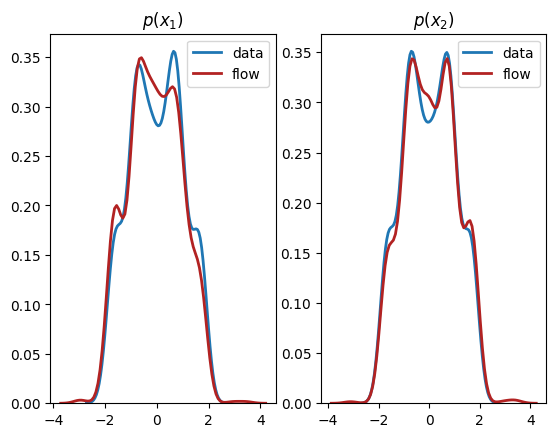
As we can see, we have learnt close approximations to the marginal distributions, . It would have been challenging to fit the irregularly shaped marginals with standard methods, for example, a mixture of normal distributions. As expected, since there is a dependency between the two dimensions, we do not learn a good representation of the joint, . In the next section, we explain how to learn multivariate distributions whose dimensions are not independent.